Biography:

M Khoshnevisan is an Associate Professor at Ajman University. He is a member of the American Physical Society. He was formally invited as a visiting scholar at the University of California-Berkeley and Harvard University during 2004-2005. He received the “Certificate of Achievement” in 2003 for his contribution to BISC FLINT-CIBI International Joint Workshop on Soft Computing for Internet and Bioinformatics from the World-renowned scientist and inventor of Fuzzy Logic, Professor Emeritus Lotfi A. Zadeh, at the University of California- Berkeley. His research interest is in Brownian motion, statistical physics, and general molecular theory of heat.

Abstract:

I have recently discovered a mathematical error in Albert Einstein’s derivation of equation 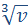=2(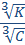) (Equation 28 in his paper, k and c are universal constants for ideal gas law and Stefan-Boltzmann law). Because of this mathematical error in the equation, his prediction of (0.420/T) for the order of magnitude of the radiation wavelengths is incorrect. I have derived the correct form of equation [28] given in his original 1904 paper, and calculated the new value for the order of magnitude of the radiation wavelengths as (0.263/T). This new value is based on the solution of the first order differential equation,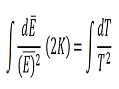for the value of Ē. The correct value of the order of magnitude of the radiation wavelengths is 0.263/T. Correcting this mathematical error indeed shows that Einstein’s prediction for the order of magnitude of the radiation wavelengths is more accurate than he thought during his life time.

Biography:

Elena Tobisch has graduated from Lomonosov’s Moscow State University in Number Theory, and has completed her PhD (Russia) and Habilitation (Austria) in Mathematical Physics. She is the Head of the Group for Nonlinear Resonance Analysis and has been awarded many prizes including V I Vernadsky Medal, 2009; Doctor H C, 2012; MiA-Award 2013. She owns one patent, has published over 100 papers in reputed journals and a few books and book chapters, including monograph published by Cambridge University Press. She created a new field of science thus allowing for the first time to explain many known physical phenomena, e.g. intra-seasonal oscillations in the Earth’s atmosphere.

Abstract:

Description of the universe in the scientific paradigm is based on conceptions of action and reaction. The main question then is, what sort of reaction should be expected to this or that action. Intuitively we expect bigger reaction to bigger action, and this is mostly the case. However, there exists a remarkable exception-the phenomenon of resonance first described by Galileo Galilei in 1638: “one can confer motion upon even a heavy pendulum which is at rest by simply blowing against it; by repeating these blasts with a frequency which is the same as that of the pendulum one can impart considerable motion”. Nowadays resonance is generally regarded as a red thread which runs through almost every branch of physics; without resonance we wouldn't have radio, television, music, etc. Horrible destructions due to the occurrence of resonance in a particular system are also well known. The demand for a good mathematical description allowing to predict the appearance of a resonance and to deduce its quantitative characteristics, is obvious. Linear resonances are easily treatable by the linear Fourier analysis while for the description of nonlinear resonances a new branch of the mathematical physics has been recently developed (a book of speaker): “Nonlinear Resonance Analysis”, with its own theory, computational methods, applications and open questions. In this lecture I shall demonstrate how nonlinear resonance analysis can be applied to a number of real systems, including large-scale phenomena in the Earth's atmosphere and novel wave turbulent regimes, and explains a range of laboratory experiments.

Biography:

Álvaro Q Valenzuela obtained his BSc in Engineering Sciences in 1974, and Electrical Engineering degree in 1977, at the University of Chile, where he taught electromagnetic fields and related subjects for more than two decades. In 1980, he joined the Chilean Air Force as a Civil Servant, where he is currently working. He has served abroad in South Africa, England and France, participating in the development of the first three Chilean satellites. In 1998 he obtained his MSc degree with distinction on Satellite Engineering at the University of Surrey. In 1994 he initiated independent research on classical extended electron models, specializing in the time invariant solutions of Maxwell equations in toroidal coordinates. The main findings of his research are summarized in the paper “The Revenge of Old Classical Physics: No Space for Photons or Relativity”, published by Galilean Electrodynamics, September-October 2009 issue.

Abstract:

As an introductory remark it is clarified that in this paper the term “classical physics”, refers exclusively to Newton´s and Maxwell equations, and does not consider special or general relativity. In the first part of this work it is shown, that the well-known claims about the ineptitude of classical physics in the microscopic domain are false, by giving simple classical interpretations for the photoelectric effect, the Compton effect the radiated spectra of the hydrogen atom and Planck´s radiation law. It is concluded that the falsehood of the previous claims, is merely a necessary – but not a sufficient –condition for the applicability of classical physics to quantum phenomena. In the second part of this work, a formal classical theory for the stable (force-free) extended particle is developed, which by considering electromagnetic and gravitational forces, leads to a nonlinear equation for the electric, magnetic and gravitational potentials. Some solutions of the basic equations for unbounded media are presented. The boundary value problem for the isolated elementary particle is formulated, and the numerical and analytical techniques that are currently being applied, in an attempt to find a solution in toroidal coordinates by successive over relaxation methods, are reviewed. It is concluded that the solution of this boundary value problem is crucial to determine the applicability of classical physics to quantum phenomena. On one hand, if it can be shown that no solution exists, then this is a rigorous proof of its inapplicability. On the other hand, if a solution is found, then to be applicable, it must also predict the mass and the spin of the electron and the proton.

Biography:

Eliade Stefanescu graduated from the Polytechnic University of Bucharest in 1970, with a specialization in Physics of Semiconductor Devices in 1976, and a PhD in Theoretical Physics in 1990. He became a Scientist in 1976, Senior Scientist 3 in 1978, Senior Scientist 2 in 1991, and Senior Scientist 1 in 1997. Since 2004 he is Senior Scientist 1 at Advanced Studies in Physics Centre of the Romanian Academy. He is known for a microscopic theory of open quantum systems, the invention and the microscopic theory of a semiconductor device for the convertion of environmental heat into usable energy, and a unitary quantum relativistic theory.

Abstract:

Our starting point is a wave packet of a quantum particle, which, for the agreement of the group velocities in the coordinate and momentum spaces with the Hamilton equations, instead of the Hamiltonian in the time dependent phase, includes the Lagrangian. We consider the interaction of such a particle with an external field, with potentials conjugated to time (the scalar potential), and to the spatial coordinates (the vector potential), and a quantum relativistic principle, asserting that the time-dependent phase of a quantum particle is an invariant for an arbitrary change of coordinates. For this field, we obtain the Lorentz equation of the particle-field interaction, the Faraday-Maxwell equation and the Gauss-Maxwell equations for the field components of the two potentials, and the Ampère-Maxwell equation for an electromagnetic field. For a nonrelativistic case, we obtain a Schrödinger equation with a Hamiltonian including the rest mass. With this equation, we obtain the spin as a characteristic of the particle wave function. From the group velocity of a particle wave packet, we obtain an acceleration,  proportional to the Christoffel symbols, which take non-zero values only in the curved space of a gravitational field.

Biography:

Vasily Yu Belashov has completed his PhD in Radiophysics and  Doctor of Science in Physics and Mathematics. His main fields includes: theory and numerical simulation of the dynamics of multi-dimensional nonlinear waves, solitons and vortex structures in plasmas and other dispersive media. Presently, he is Professor in the Kazan Federal University. He was Coordinator of studies on the International Program Solar Terminator (1987-1992), and took part in Programs WITS/WAGS and STEP. He is author of 288 publications and books: “Solitary Waves in Dispersive Complex Media: Theory, Simulation, Applications”, Springer-Verlag GmbH, 2005; “The KP Equation and its Generalizations. Theory and Applications”, Magadan, NEISRI FEB RAS, 1997.

Abstract:

The results of numerical study of evolution and interaction of the vortex structures in a continuum and specifically, in plasmas and fluids in 2D approach, when the Euler-type equations are valid, are presented. The set of the model equations 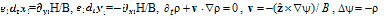describing the continuum or quasi-particles with Coulomb interaction models, where r is a vorticity or charge density and y is a stream function or potential for inviscid fluid and guiding-centre plasma, respectively, and H is the Hamiltonian, was considered. For numerical simulation the CD method specially modified was used. The results showed that for some conditi­ons the interaction is nontrivial and can lead to formation of complex forms of vorticity regions, such as the vorticity filaments and sheets, and also can be ended to form the turbulent field. The theoretical explanation of the effects is given on the basis of the generalized critical parameter which determines qualitative character of interaction. We investigated the applications of the results to dynamics of vortex structures in the atmosphere, hydrosphere and plasma, namely: evolution of the cyclonic type synoptic and ocean vortices which can be considered as a vorticity front, and interactions in the vortex-dust particles system, and also dynamics of charged filaments which represent streams of charged particles in a uniform magnetic field in 2D model of plasma of Taylor-McNamara. Our approach may be effective in studying of the atmospheric and Alfvén vortex dynamics, and useful for the interpretation of effects associated with turbulent processes in fluids and plasmas.

Biography:

Abstract:

Three dimensional self-modulated dynamics of a relativistic charged particle beam is reviewed within the context of the theory of plasma wake field excitation. The self-consistent description of the beam dynamics is provided by coupling the Vlasov equation with a Poisson-type equation relating the plasma wake potential to the beam density. An analysis of the beam envelope self-modulation is then carried out and the criteria for the occurrence of the instability are discussed thereby.

Biography:

Dominique Ausserré has completed his PhD in Collège de France, Paris and has been Visiting Scientist in IBM, San Jose. He is a co-starter of a soft matter lab in Institut Curie, Paris, and then moved to Le Mans University in 1991. He is Research Director in CNRS, France, and worked in the fields of optics, polymer and statistical physics, material science, capillarity and surface physical chemistry, now moving towards biology and healthcare oriented technological developments. He invented self-assembled nano-composite materials made of nanoparticles and diblock copolymers, self-assembled polar lamellar materials named ferrochemicals, and the SEEC and BALM optical techniques. He was Co-founder of two startups : Nanoraptor and Watch Live.

Abstract:

An irreversible phenomenon are characterized by a monotonic parameter of (universal) time t. According to philosophers, time cannot be defined without a reference to itself. We contest this because time is also a monotonic function of any irreversible parameter, from which time can be defined as well. Since universe expansion is a commonly accepted irreversible process, the average density of the universe 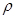 is a good candidate. Therefore we can define 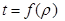. Then the choice of the monotonic (and continuous) function f is open. In the absence of additional requirement, we can defnine A time 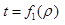and another time 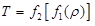. Additional requirements will come from some physical hypothesis, such as inertia priniciple. It is a physical axiom, hopefully coherent with our everyday intuition and vocabulary. Every alternative definition of a time will lie on different physical rules and lead to different physical equations. Simpler than defining time is switching from one time to another. One can chose such a tranformation f₂ (we will say mapping) in order that the impact on our equations is minimal at the human scale, which means in order that the two times t and T coincide over the short period of our existence. I will propose such a tranformation. It has amazing effects: for instance, within time T, the age of the universe becomes infinite. Beside a playful attempt to introduce some doubt in the apparently safest conceptual areas, the goal of this talk is to get the feedback of experts in astrophysical and comological models about the connexions they can infer between such time manipulation and the fundamentals of their models.

Biography:

Eliza Wajch completed her PhD from Lodz University in 1988 and her habilitation in Poland in 1998. She is a Mathematician working on topology, axiomatic foundations of mathematics and applied mathematics. She attends seminars on foundations of physics at the Centre of Theoretical Physics of the Polish Academy of Sciences in Warsaw. She is an Author or Co-author of over 30 articles and one book. Presently she is working as an Associate Professor at the Institute of Mathematics and Physics of Siedlce University of Natural Sciences and Humanities in Siedlce, Poland.

Abstract:

A significant progress in the development of an axiomatic quasi–set theory (QST) and its application in quantum physics, where indistinguishability and non-individuality appears has been made by Décio Krause and others. I offer a sketch of a modification of QST to quasi-classes theory (QCT) such that proper quasi-classes can be considered as existing objects, while ZF minus the postulate of infinity can be treated as a sub theory of QCT. It is not claimed that infinite collections certainly exist in QCT. None of the known forms of the axiom of choice is an axiom of QCT. Every quasi-set of QCT is a quasi-class of QCT. To avoid inconsistencies, it is assumed that a quasi-class which is not a quasi-set cannot be an element of a quasi-class. Notions of D-countability and D-uncountability that need not refer to numbers can be considered in QCT. The primitive concept of a quasi-cardinal (qc) in QST can be investigated deeper in QCT than in QST. Intuitively, qc (x) is a cardinal number of ZFC which is assigned to a quasi-set x to stand for the ‘quantity’ of elements of x. New arguments that the concept of qc is not precise enough have been found recently. Modifications of qc are needed to give more satisfactory answers to questions about, in a sense, how large a quasi-set can be and how many elements it can have.

Biography:

Anatoly Shabad is educated from Moscow State University (1956-1962). He acquired his Candidate of Science (1968) and Doctor of Science (1986) degrees in P N Lebedev Phys. Inst., Russian Academy of Sciences. He is affiliated with this institute since 1965, now as Principal Researcher of I E Tamm Dept. of Theor Phys. He served two terms as a Deputy to the Parliament of the Russian Federation, 1990-1996, was a supporter of the Yeltsin-Gaidar reforms. His works are in the fields of quantum mechanics, optics, quantum theory of gauge fields and quantum plasma theory. His main achievements relate to nonlinear effects associated with quantum electrodynamics with strong external fields. Among these are the photon capture by magnetic field of a pulsar, accompanied by formation of a mixed state between the photon and the positronium atom, renormalization of the magnetic and electric dipoles of elementary particles due to the self-interaction of their electromagnetic fields, presence of a magnetic response to an electric source in external fields, especially in the form of a magnetic monopole. Also an upper bound possible value of the magnetic field is found to be supplied by the phenomenon of collapse of positronium in a strong magnetic field.

Abstract:

Since the ancient times, people have been wondering why there is no such thing as a magnetic pole, why every magnet, including the Earth itself, is a dipole with two poles, and why nobody succeeded to cut a magnetic dipole into two halves, carrying only one type of magnetic charge each, northern or southern. This fact becomes more interesting after one inspects the basic Maxwell equations of electrodynamics that readily admit inclusion of magnetic charges on the same ground as the well-known electric charges. However, Paul Dirac established that a magnetic monopole cannot exist alone: it must be supplemented by what is now called the Dirac string–an infinitely thin solenoid, which canalizes all the magnetic lines of force diverging to the monopole outwards. Later he established that quantum mechanics states that if at least one magnetic monopole exists in the whole world, all electric charges would have discrete values. If we accept the charge of the quark, the smallest constituent of matter, to present the necessary quantum of charge, the corresponding value of the magnetic charge would be tremendous. However, up to now no magnetic charge has been discovered anywhere in nature. The reason may be that the magnetic charge is a very special object, called a pseudo-scalar, the scalar that changes its sign under reflection in a mirror. No fundamental object of this sort is known, but it can be readily constructed as the scalar product of a magnetic and electric fields. Therefore, to build a magnetic monopole one might try to combine multiplicatively an electric monopole with these two fields. However, the classical electrodynamics of Maxwell and Faraday admits only linear combinations of fields, the fields are independent and they do not influence each other. The situation becomes different when quantum electrodynamics by Feynman and Schwinger comes into play. In that theory the quantum of electromagnetic field, photon, creates virtually a pair of electrically charged particles, electron and positron, that later annihilate back to a photon. But, while existing in the state of the charged particles, the photon might interact with other electromagnetic fields and with itself. This is how, in quantum theory, electromagnetic fields interact between themselves. Correspondingly, the modified Maxwell equations become non-linear already in the vacuum. If we place a point-like electric charge into a combination of constant electric and magnetic fields with non-zero scalar product between them, the non-linear Maxwell equations produce the magnetic response, which carries a single point-like magnetic charge. Unlike the Dirac monopole proper, this one, cooked of ordinary fields, is not spherically symmetrical. It has two Dirac strings stretched along the above electric and magnetic fields, which merge to one if these fields are parallel. However, this modified monopole cannot serve to establish the discreetness of electric charges in Dirac’s way. Hence the problem raised by his consideration remains unsolved, although a magnetic monopole has been made.